SOLUCIÓN DEL SUDOKU

Os dejo la solución del sudoku que hemos hecho en clase para que podáis corregirlo en casa:

Fuente: Ana García Azcárate

Razones trigonométricas de los principales ángulos

Os pongo el vídeo que comenté en clase sobre las razones trigonométricas de los principales ángulos, un vídeo de Unicoos que se que siempre os gustan.

Vídeo de razones trigonométricas de un ángulo cualquiera

Razones trigonométricas de un ángulo agudo

HOLA CHIC@S!! Hoy en clase hemos hablado sobre las razones trigonométricas de un ángulo agudo;

¡¡OJO!!  EL SENO Y EL COSENO PUEDEN SER COMO MÁXIMO 1.

EJEMPLO:
Dado este triángulo calcula sus razones trigonométricas del ángulo B.
a=hipotenusa   b= cateto opuesto  c=cateto contiguo

$$seno(senB)=\frac { cateto\quad opuesto }{ hipotenusa } =\frac { 4 }{ 5 }$$
$$coseno(cosB)=\frac { cateto\quad contiguo }{ hipotenusa } =\frac { 3 }{ 5 }$$
$$tangente(tgB)=\frac { seno }{ coseno } =\frac { cateto\quad opuesto }{ cateto\quad contiguo } =\frac { 4 }{ 3 }$$

INVERSAS

$$cosecante(cosecB)=\frac { 1 }{ seno } =\frac { hip }{ cat.\quad opuesto } =\frac { 5 }{ 4 }$$
$$secante(secB)=\frac { 1 }{ coseno } =\frac { hip }{ cat.\quad contiguo } =\frac { 5 }{ 3 }$$
$$cotangente(cotgB)=\frac { 1 }{ tangente } =\frac { cat.contiguo }{ cat.\quad opuesto } =\frac { 3\sin ^{  }{  }  }{ 4 }$$


DEBERES
PG.101 ej. 8
PG.102 ejs.13-15
PG.103 ej.18

Teoremas de la altura y del cateto

HOLA CHIC@S, Hoy en clase hemos aprendido dos teoremas; el del cateto y el de la altura y los radianes;









TEOREMA DE LA ALTURA

En un triángulo rectángulo, el cuadrado de la altura sobre la hipotenusa coincide con el producto de las proyecciones de los catetos sobre la hipotenusa.
Fórmula;




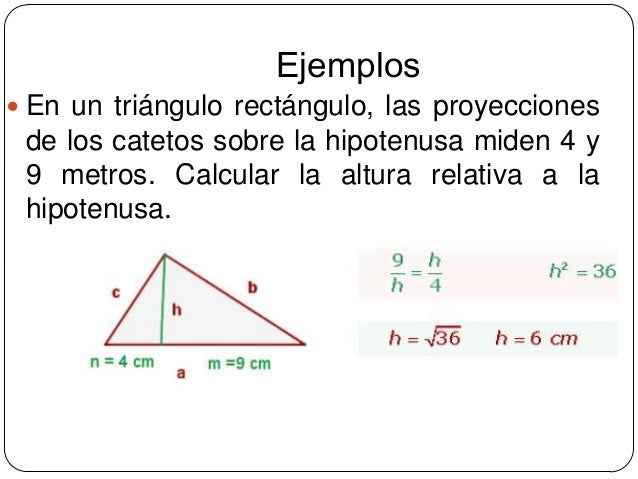
TEOREMA DEL CATETO
En un triángulo rectángulo, el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección de dicho cateto sobre la hipotenusa
Fórmula;




ATENCIÓN; ESTAS DOS FÓRMULAS SÓLO SE PUEDEN APLICAR A TRIÁNGULOS RECTÁNGULOS

RADIANES (MEDIDAS DE ÁNGULOS)
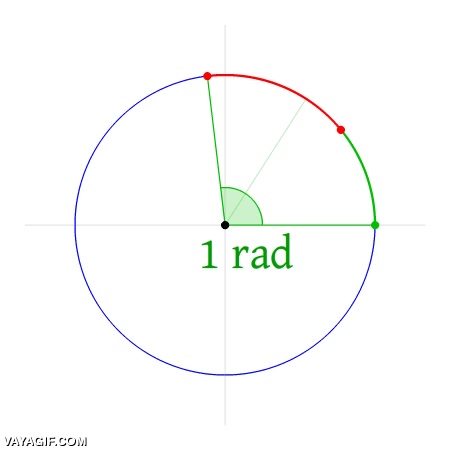
Radianes(rad); un radián es la medida del ángulo central de una circunferencia cuyo arco coincide con la longitud del radio.

grados= sistema sexagesimal

1º=60'
1'=60''






RELACIÓN ENTRE GRADOS Y RADIANES

180º= 3,1416 rad
360º=2x3,1416 rad
90º=3,1416/2 rad



Hoy no tenemos deberes!!

criterios de semejanza de triángulos

Tema 5: Semejanza y Trigonometría

Hola a todos hoy en clase hemos corregido los ejercicios 45, 47, 48, 49, 52, 54 y 55 de la página 112 del libro.

Criterios de semejanza de triángulos:

  

    -Dos triángulos son semejantes si:

                 

                   1. Tienen dos ángulos iguales

                   2. 1 ángulo igual y los lados que lo forman son proporcionales

                   3. Tienen los tres lados proporcionales

   

Video teorema de catetos y altura

Tema 5: Semejanza y Trigonometría

Hola a todos en la clase de hoy hemos visto; ¿Qué son las figuras?¿Qué es el problema de Tales?        ¿Cuando decimos que algo es semejante?...

1.Figuras semejantes. 

 Tiene misma forma pero distintas dimensiones.

El cociente de la distancia de 2 puntos en una figura entre sus homólogos es constante: razón de semejanza.

¿Qué es un homólogo? 

El punto homólogo de C' es C el de A' es A ...

¿Que es la razón de semejanza?  

 Cogemos dos puntos cuales quiera de cada figura. 

La razón de semejanza (K): cogemos dos puntos (AD) lo cual nos fijamos en sus lados homólogos (A'D') y estos los dividimos, en este ejemplo nos daría que la razón es 0,6. Por otra parte puede salir otra respuesta según lo que tomemos de referencia si yo cojo ahora del mayor al menos me saldría A'D'/AD y con los datos del ejemplo daría 1,5.

2.Polígonos semejantes. 
1- Tienen el mismo número de lados
2-Ángulos homólogos son iguales (no nos confundamos con el rombo y el cuadrado , no tienen los ángulos iguales)
3- Los lados homólogos son proporcionales

3.Razones (k) entre figuras semejantes.
k= razón entre los lados homólogos
k^2=razón de las áreas
k^3=razón de los volúmenes

Teorema de tales.

¡¡DEBERES!! PÁG 99 Nº 1,3,4,5