En primer lugar, tenemos que recordar qué es un vector libre. ¿Os acordáis que lo dimos hace poco? Era una especie de representante de un conjunto de vectores equipolentes. Vamos a usar los vectores:
u ⃗ = (u₁, u₂)
v ⃗=( v₁, v₂)
#Suma de vectores libres
Algebraicamente:
u ⃗ +v ⃗ =(u₁+v₁, u₂+v₂)
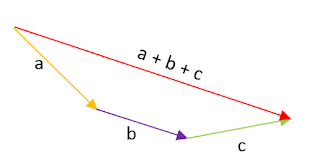
Geométricamente:
Aclaración: las coordenadas de un punto nos indican cuánto se mueven hacia la izquierda/derecha y arriba/abajo no el punto de comienzo ni de final.
#Producto de un número por un vector
Nº: K€R
K u ⃗ = K (u₁, u₂)= (Ku₁, Ku₂)
Al hacer esta multiplicación, el módulo va a cambiar ( si multiplicamos por 1 no). Además, si lo multiplicamos por un número negativo, cambiará el módulo pero también el sentido.
#Combinación lineal de vectores
Dos vectores,u ⃗ y v ⃗, son linealmente dependientes (l.d) si tienen la misma dirección y sus coordenadas son proporcionales.
- Ejemplo 1 :
u ⃗ = (2,4)
v ⃗ = (1,2) Por lo tanto... u ⃗= 2 v ⃗ sí son l.d
u ⃗= 2 v ⃗ sí son l.d
- Ejemplo 2:
u ⃗ = (2,4)
v ⃗ = (-1, -2) Por lo tanto... u ⃗= -2 v ⃗ sí son l.d
u ⃗= -2 v ⃗ sí son l.d
- Ejemplo 3:
u ⃗ = (2,4)
v ⃗ = (-1,2) Por lo tanto... NO son linealmente dependientes
Combinación lineal (c.l): El vector w ⃗ es combinación lineal de los vectores u ⃗ y v ⃗ si se pueden encontrar números reales tales que: w ⃗= au ⃗ + b v ⃗
w ⃗ es combinación lineal de los vectores u ⃗ y v ⃗ si se pueden encontrar números reales tales que: w ⃗= au ⃗ + b v ⃗
Ejemplo:
¿w ⃗(3,4) es l.d de u ⃗ (1,0) y v ⃗ (0,1)?w ⃗= 3(1,0) + 4( 0,1) = (3,0) + (0,4)= (3,4) TAREA: Pg 139 ejs 8, 9, 11.
Además, recuerdo que el examen global de la 2ª evaluación es el miércoles 28 de marzo (dentro de una semana). Hay que estudiar desde los sistemas de ecuaciones hasta el tema anterior a los vectores ( los vectores no entran en esta evaluación?
¡Hasta mañana!
No hay comentarios:
Publicar un comentario