Hoy en clase lo 1º de todo hemos corregido la tarea (ej 35 y 36 pag 101) y después Bego nos ha explicado los sistemas de ecuaciones no lineales:

SISTEMAS DE ECUACIONES NO LINEALES

Ejemplo:

1º Empezamos el sistema como empezaríamos cualquier otro.

2º Cuando tengamos una ecuación de 2º grado la reorganizamos como tal.

3º Utilizamos la formula de las inecuaciones.

4º Sustituimos la otra ecuación del sistema para hallar la otra incógnita.

5º Fin.

Tarea para el viernes: Pág 98 ej 13

METODOS DE RESOLUCIÓN DE SISTEMAS

Hola a todos!

Bueno ayer viernes lo primero que hicimos fue corregir la tarea del día anterior como siempre y preguntarle dudas, si las ha habido.

Despues vimos los diferentes metodos de resolucion de sistemas que hay.

Aquí os dejo los 4 métodos de resolucion de sistemas:

Como pone en la imagen de ariba puede que:

• Tengan una solución única
• No tengan solución
• Infinitas soluciones

Bueno pues esto es lo que vimos ayer. De tarea mandó los ejercicios:
35 y 36 de la página 105.

BUENO QUE PASEIS BUEN FINDE!!!

Problemas día 20.

Buenas gente!

Bueno, pues como todos los jueves, hemos estado haciendo un problema en clase.

El problema ya está en otra entrada explicado el enunciado y todo lo que hay que saber, a si que no me seáis vagos, y mirar la otra entrada si os es necesario.

Bueno, dicho esto voy con la formula correcta y os la explico un poco.

La formula para hallar los movimientos es:

explicada seria:

número de bolas de cada color por número de bolas de cada color menos uno partido dos.

Ponemos un par de ejemplos para ver que la formula es correcta.

Para poner los ejemplos os voy a poner una tabla:

vamos a comprobarlo:

Si tenemos dos bolas de cada color seria:

2(2-1)=2

2/2= 1 movimiento.

Si tenemos 16 bolas de cada color seria:

16(16-1)=240

240/2=120 movimientos.

Si tenemos 33 bolas de cada color seria:

33(33-1)=1056

1056/2=528 movimientos.

Si tenemos 50 bolas de cada color seria:

50(50-1)=2450

2450/2=1225 movimientos.

Bueno y con esto termino.

Os dejo la tarea otra vez por si alguien no la ha echo todavía:

De la página 89 el ejercicio 62 e, f, g y h

De la página 104 el ejercicio 30 c y d y el 33

CORRECCIÓN TAREA.

Hoy en clase hemos corregido la tarea de ayer. Os pongo las correciones. ( Cuando ponga " ^ " significa elevado que nosé ponerlo y cuando quiera decir mayor/menor o igual pondré <- , o >-) ( más menos .. será +-) ( Raíz es "R" )

-Página 89-

.Ejercicio 62.

a) x^2 -1 >- 0

x^2 -1 = 0
x= o+-R 0^2 -4 (-1) = 0+- R4 = 0+-2 = 1,-1

2 2 2

Cogemos los puntos -2, 0 y 2

(-2)^2 -1 >- 0

3>-0 el -2 SI

0^2 -1 >- 0

-1 >- 0 el 0 NO

2^2 -1 >- 0

4-1 >- 0

3>- 0 el 2 SI

Solución: (- infinito,-1] U [1, +infinito)

b) ( x-2) (x+3) > 0

(x-2) (x+3) = 0

x-2 = 0 - - - > x = 2

x+3 = 0 - - - > x = -3

Cogemos los puntos -4 ,0 y 3

(-4 -2) ( -4 +3) > 0 el -4 SI

(0 -2) (0 +3) > 0 el 0 NO

(3 -2) (3+3) > 0 el 3 SI

Solución: ( - infinito, -3) U (2, +infinito)

c) x^2 -4 <>

x^2 = 4

x = R4

x = 2, -2

Cogemos los puntos -3, 0 y 3

-3^2 -4 <>

9 -4<>

5 < style=""> el -3 NO

0^2 -4 <>

-4 < style=""> el 0 SI

3^2 -4 <>

9 -4 <>

5 < style=""> el 3 NO

Solución: ( -2, 2 )

d) x(x+5) <_0 x =" 0" 5 =" 0" x =" -5">

36 -30 <_>

6 <_ style=""> el -6 NO

-4 ( -4 +5) <_>

16 -20 <_>

-4 <_ style=""> el -4 SI

1(1 +5) <_>

1+5 <_ style=""> el 1 NO

Solución: [-5,0]

-Página 104-

.Ejercicio 30.

a)

x+y = 10

2x +y = 20

Por el método de reducción.

2x + 2y = 20

2x +y = 20

Y = 0

X + 0 = 10

X = 10

Solución: y = 0, x = 10

b) x+y = 10

2x -2y = -20

Por el método de sustitución.

X = 10 –y

2(10 –y) -2y = -20

20 -2y -2y = -20

-2y -2y = -20 -20

-4y = -40

Y = 10

x = 10 –y

x = 10-10

x = 0

Solución: y = 10, x = 0

Espero que lo hayáis entendido y sino mirad los resultados y lo hacéis vosotros ; )

Y hacer la tarea que es:

Página 89, ejercicio 62,e,f,g,h

Página 104, ejercicio 30,c,d y 33

Inecuaciones de segundo grado

Bueno chavales,
hoy en clase hemos aprendido a hacer iencuaciones de segundo grado, que son muy faciles, son iguales que las inecuaciones normales solo que tenemos que comprobar con dos resultados.
Bien, una vez dicho lo que voy a explicar , me pongo a ello.
Lo primero que debemos hacer es igualar a cero la ecuación despues ponerla en estructura de ecuación de sgundo grado y después resolver. una vez hecho todo esto lo que tenemos que hacer es representar los dos puntos en la recta y comprobar, si a la izquierda de el primer numero sirven los resultados , si a la derecha del sguno sirven y si entre ambos sirven los resultados. La solución se expresa igual que con las de primer grado solo que en estas , si hace falta , se pone unión.
Ejemplo:
x²-3x ≥ 4
Igualamos a 0
x²-3x = 4
Odenamos en forma de ecuación de segundo grado
x²-3x-4 = 0
aplicamos la formula y resolvemos
x=(3±√9+16)/2
x=(3 ± 5) /2
x=4
x=-1
Y ahora hacemos lo de comprobar:
x²-3x ≥ 4
-2²-3.-2 ≥ 4
4+6≥4
10≥4
Con -2 si se da por lo tanto a la izquierda del -1 seran todos
x²-3x ≥ 4
0²-3.0 ≥ 4
0≥4
Con el 0 no por lo tanto los de el medio no los cojemos, por eso ponemos unión
x²-3x ≥ 4
5²-3.5 ≥ 4
25-15≥4
10≥4
Se cumple asique los de la derecho también son todos
Bien una vez tenemos los dos resultados pasamos a lo de la recta.
adjunto lo que seria el dibujo de la recta.

y entonces los intervalos quedarian así: (-∞,-1] U [4, ∞)

La tarea que ha mandado bego es página 89 ejercicios 62 a,b,c,d y página 104 ejercicio 30 a,b

Bueno y mi toque personal!

Pues nada informaros de que Angel Martín deja Se lo que hicisteis , un programa que no muchos seguireis pero que lo habries visto alguna vez . Bueno pues he aqui mi pequeño ``homenaje´´ a este gran humorista que se va de la televisión porque dice que esta cansado... En fin deciros que mañana jueves es el último día que podreis verlo en se lo que hicisteis y que el domingo va a ir a El club de la comedia programa que se emetirá a las 21:30 en la sexta ! Un saludo y pasadlo bien!
Pd: Angel es este la rubia de al lado es Patricia

Fuente : http://www.20minutos.es/imagen/541489/

INECUACIONES

Problema

CLASIFICACIÓN

En una línea a lo largo del suelo están colocadas 50 fichas rojas y 50 azules alternativamente: RARARARA…RARARA

Permutando fichas consecutivas hay que clasificarlas en dos grupos, con todas las fichas rojas a un lado y todas las azules a otro:

RRRR…AAAA

· ¿Cuál es el menor número de movimientos necesario para hacerlo?

· ¿Cuántos movimientos se necesitarán para n fichas azules y n rojas?

· ¿Qué ocurre cuando la posición inicial de las fichas es diferente?

Por ejemplo: RRAARRAA...RRAA

RAARRAARR…RAAR

· ¿Qué ocurre cuando hay fichas rojas, azules y verdes colocadas: RAVRAV…RAV ?

· ¿Qué ocurre con 4 colores?

Por si os atascáis……..

INDICACIONES/CONSEJOS

· Intenta algunos casos sencillos, es decir intenta con menos fichas.

· Sé sistemático, intenta mover las fichas sistemáticamente.

· Busca una representación adecuada. Intenta usar fichas reales sino busca un sustituto. ¿Puedes usar los casos más sencillos que ya has resuelto para generar otros casos?

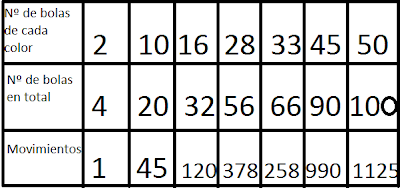
· Haz una tabla, que muestre la relación entre el número de fichas y el de movimientos.

· Busca una regla con tu representación, para cualquier número de fichas.

· Comprueba tu regla con números pequeños y grandes.

ESTO HE HECHO YO:

1. Probé con pocas fichas y a raíz de ahí construí una tabla y me quedó así:

Número de bolas . Movimientos , de aquí saco que la diferencia es

4................................ 1

6 ................................3..................................... = 2

8 ................................6 .....................................= 3

10 ..............................10 ...................................= 4

12 ..............................15 ...................................= 5

14 ..............................21................................... = 6

16 ..............................28 ...................................= 7

18 ..............................36 ...................................= 8

20 ..............................45 ...................................= 9

22 ............................. 55 ...................................= 10

24 ..............................66 ...................................= 11

26 ..............................78 ...................................= 12

28 ..............................91 ...................................= 13

30 ............................105 ...................................= 14

32 ........................... 120 ...................................= 15

34 ............................136 ...................................= 16

36 ............................156 ...................................= 17

38 ............................174 ...................................= 18

40 ............................193 ...................................= 19

42 ............................213 ...................................= 20

44 ............................234 ...................................= 21

46 ............................256 ...................................= 22

48 ............................279 ...................................= 23

50 ............................303 ...................................= 24

52 ............................328 ...................................= 25

54 ........................... 354 ...................................= 26

56 ............................381 ...................................= 27

58 ............................409 ...................................= 28

60 ............................438 ...................................= 29

62 ............................468 ...................................= 30

64 ............................499 ...................................= 31

66 ............................531 ...................................= 32

68 ............................564 ...................................= 33

70 ............................598 ...................................= 34

72 ............................633 ...................................= 35

74 ............................669 ...................................= 36

76 ............................706 ...................................= 37

78 ............................744 ...................................= 38

80 ............................783 ...................................= 39

82 ............................823 ...................................= 40

84 ............................864 ...................................= 41

86 ............................906 ...................................= 42

88 ............................949................................... = 43

90 ............................993 ...................................= 44

92 ..........................1038 ...................................= 45

94 ..........................1084 ...................................= 46

96.......................... 1131 ....................................= 47

98 ..........................1179 ....................................= 48

100 ........................1228 ....................................= 49

Solución: 1228 movimientos para las 100 bolas.

La ecuación no la sé hacer aún pero espero que con esto podáis resolverlo. (:

Ecuaciones con radicales.

Hola clase! (:

Bueno lo que hicimos el miércoles 12.01.2011 fue:

Ecuaciones del tipo (x-a) . (x-b) .... = 0

Ej:

Ecuaciones con fracciones algebraicas

Bueno creo que esto fue todo.

En cuanto a la tarea, si mal no recuerdo fue:

Pàgina 80 ejercicios 15 y 16.

El Kakapu

Para que os riáis un poquillo

Fuentes: http://www.youtube.com/watch?v=407GlN3rn9Q&feature=player_embedded

¡Pedazo de poema!

naranjas naranjas
limones limones
x mas cinco
son 5 millones.

¿que numero es?

x + 5 = 5.000.000
x = 5.000.000 - 5
x = 4.999.995

Editor de ecuaciones

Bueno aquí os dejo un editor de ecuaciones que lo que haces es que al escribir tu una ecuación en él lo convierte en una imgen . http://www.alciro.org/tools/matematicas/editor-ecuaciones.jsp
Y ahora que estamos con ecuaciones,inecuaciones y sistemas de ecuaciones yo creo que os irá bien!
La forma de utilizarlo es simple.
Escribis lo que querais en el recuadro que hay alí

Y a continuación pulsais render

Yo por ejemplo he escrito x-5=6 y al pulsar render esto es lo que aparece:

Clickais con el boton derecho del raton encima de la formula y le dais guardar imagen como. Después os pondra que la iamgen se llama text podeis cambiarle el nombre si quereis pero lo que si que os recomiendo que hagais es que escribais despues del nombre esto : .jpg eso es para descargarla directamente en jpg y subirla al blog mas facilmente.

Una vez hecho esto no teneis mas que subir la iamgen en vuestra entrada y listo :)
Os pongo la imagen de mi formula ya descargada para que veais como queda:


Un Saludo!

POEMA DE LOS NUMEROS

1.- El fragmento en donde se encuentra la ecuacion es el último:

'Pues si mi propia raíz Cuadrada

a mi mismo me restan,

por una gracia solo a mi reservada

el resultado es justo treinta'

• La ecuacion es:

4: NÚMEROS IMPORTANTES:

• La constante matemática e es uno de los más importantes números reales.¹ Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial f(x) =e^x es esa misma función. El logaritmo en base e se llama logaritmo natural o neperiano.

El número e, conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemático escocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.

• π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un numero irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:

El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Por ello, tal vez sea la constante que más pasiones desata entre los matemáticos profesionales y aficionados. La relación entre la circunferencia y su diámetro no es constante en geometrías no euclídeas.

CONCURSO MATEMÁTICO-LITERARIO

Ya estamos de vuelta otra vez a la rutina... Para empezar bien la cosa, os voy a comentar que hay un concurso al que os podéis apuntar.Está organizado desde el departamento de Matemáticas de la Universidad de La Rioja. Es, como dice el título de la entrada, un concurso matemático-literario que consiste en:

 - Leer la novela "El rescoldo", de Joaquín Leguina, ambientada en los años previos a la Guerra Civil española y en la que uno de los protagonistas es matemático.
-  En el libro de Joaquín Leguina El rescoldo aparecen varios matemáticos con sus nombres modificados.
 Eligir uno de ellos y averiguar su nombre real. Hacer una biografía novelada, de entre cuatro y diez páginas, sobre la vida y obra del matemático elegido.
 - Resolver el problema siguiente: Dado a un número racional, encontrar todos los números racionales x, y de modo que sumando el cuadro de x con el cuadrado de y obtengamos el cuadrado de a; o sea*



Os animo a participar, ya que es bastante interesante. Podéis obtener mas información pinchando aquí.

Ah, se me olvidaba, los premios son de 500, 300 y 200 euros...

Te Limpiamos La Pantalla Gratis