Como veis, después de unas vacaciones, que se nos han hecho muy cortas, volvemos a la normalidad, y vuelta al blog! jajaja
Y hoy en clase lo que hemos hecho es empezar a corregir la tarea.
Era estudiar varias gráficas, y aquí voy a dejar las que hemos visto.
1º

1: Dom f = (- ∞ , 0] U [2, 5] U [6 , ∞)
Im f = [-1 , ∞)
2: Es discontinua. Continuidad = (- ∞ , 0] U [2, 5] U [6 , ∞)
Ptos discontinuidad = x=0 ; x=2 ; x=5 ; x=6
3: Cortes con los ejes -- eje x = (0,0) , (6,0)
eje y = (0,0)
4: Signo = (- ∞ ,0) : +
(2,5) : -
(6, ∞ ) : +
5: No es simétrica ni periódica
6: Creciente = (6,0) Máx = NO
Decreciente = (-∞,0) Min = (0,0) , (6,0)
Constante = (2,5)
7: Concavidad ( U) = (-∞, -3'5) U (-2'5,-1'5) U (6,6'5) U (7'5,8'3)
Convexidad = ( 3'5,-2'5) U (-1'5,0) U (6'5,7'5) U (8'3, ∞)
Ptos de inflexión = (-3'5,-1'4) ; (-2'5,1) ; (-1'5, 0,7) ; (6'5,0'5) ; (7'5,1'2) ; (8'3,2'4)
8: Como tenemos la gráfica dada, no es necesario hacer una tabla, pero en ese caso sería dar valores a la "x" y, mirando la gráfica, poner su correspondiente "y".
2º
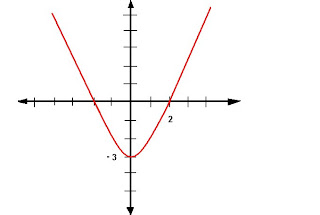
1: Dom f = R (todos los números reales)
Im f = [-3, ∞)
2: Es continua
3: Cortes con los ejes -- eje x = (-2,0) , (2,0)
eje y = (0, -3)
4: Signo = (-∞, -2) : +
(-2,2) : -
(2,∞) : +
5: Es simétrica respecto al eje "y".
No es periódica.
6: Creciente = (0, ∞)
Decreciente = (-∞, 0) Min = (0, -3)
7: Concavidad (U) = R (todos)
3º

1: Dom f = R
Im f = [-2,2]
2 : Es continua
3: Cortes con los ejes -- eje x = (-5 ,0) , (-2'5,0) , (0,0), (2'5,0) , (5,0)
eje y = (0,0)
4: Signo = + , - , +, - ...... cada 2'5
5: Es simétrica respecto al origen.
Es periódica de periodo 5, es decir, cada 5 puntos se repite todo el rato.
Bueeeeno, pues aquí nos hemos quedado en la clase de hoy.
Asi que mañana seguiremos corrigiendo chic@s!
Por lo tanto, hoy sin tarea :D
No hay comentarios:
Publicar un comentario