HOMENAJE A BARRICADA

Un poco de cultura musical, aunque tenéis exámenes estos días así que... :)
El sábado 4 en Ansoain homenaje a Barricada. Podéis ver tooooodo lo que hay aquí.

FUNCIONES DE PROPORCIONALIDAD INVERSA

Correccion de las actividades y teoria del viernes...

SENCILLÍSIMO PROGRAMA ONLINE PARA FUNCIONES

Os dejo el enlace a un programa Online function grapher que os permite dibujar funciones en 2D.
Simplemente tenéis que introducir la función en el espacio reservado para ello y la dibuja. Se puede guardar como jpg, por lo cual os puede ayudar mucho para hacer gráficos para el blog de forma muy sencilla.
Como ejemplo os pongo la gráfica de f (x) = x^2 + 2


  f(x)=x2+2

El tablero de ajedrez

Hoy como la mayoría de los jueves, hemos hecho problemas. Esta vez nos ha tocado uno en el que te tienes que entretener un gran rato para conseguir descubrir la cantidad de cuadros, rectángulos y triángulos que hay. Como hemos trabajado bastante y hemos estado callados, Bego no ha recogido el problema al final de clase, eso sí, si hay alguien que quiera mejorar su nota pues ¡que se lo entregue!

Bueno aquí os dejo algunas respuestas!

¿Cuantos cuadrados hay en un tablero de ajedrez de 8 x 8?

(tablero)

Para poder resolver esta pregunta, lo mejor es que os organicéis haciendo una tabla, así que, aquí os dejo una:

1x1	64 cuadrados
2x2	49 cuadrados
3x3	36 cuadrados
4x4	25 cuadrados
5x5	16 cuadrados
6x6	9 cuadrados
7x7	4 cuadrados
8x8	1 cuadrado

Total 204 cuadrados

¿Cuantos rectángulos hay en el tablero de ajedrez?

En esta pregunta muchos nos hemos equivocado porque al final , en el total de rectángulos no les habíamos añadido los cuadrados, que al parecer, son un tipo de rectángulo. Entonces salen 1094 rectángulos +204 cuadrados que son: 1296 rectángulos

El tercer apartado , el de la fórmula, no lo he conseguido resolver , así que si alguien lo sabe, que lo escriba en comentario o que nos lo diga en clase!

Bueno esto es todo!

Martes, 17 de Mayo de 2011

Hola, aquí os dejo lo que hemos hecho hoy en clase.
Hoy hemos ido al aula de informática para hacer un problema, pero no me acuerdo de la pagina asi que os dejo las 5 primeras preguntas:

1. Abre la llave de paso del grifo y modifica el caudal como estimes conveniente. ¿Cuál es el máximo caudal del grifo? ¿Y el mínimo? ¿Qué ocurre con el tiempo de llenado del recipiente cuando variamos el caudal?
2. selecciona un caudal de 0.5l/s y haz clic sobre el botón "poner a cero". ¿Cuánto tiempo tarda en llenarse el recipiente? Para medirlo, haz clic sobre el mismo botón "Iniciar" y vuelve a hacer clic sobre el mismo botón en el justo instante que se complete el llenado.
3. ¿Cuál es el volumen del recipiente que has llenado? ¿Cómo lo has calculado?
4. Selecciona un caudal de 0.2l/s y repite el proceso de medición del tiempo de llenado. Haz lo mismo para un caudal de 0.8l/s y para un caudal de 0.25l/s.
5. ¿Qué relación encuentras entre el tiempo de llenado del recipiente y el caudal del grifo? Sin hacer la medición, ¿Cuánto tiempo tardaría en llenarse el recipiente si el caudal fuese de 1l/s Calcula el resultado haciendo la medición correspondiente.
6. ...

Siento no poder poneros todas pero yo me quede en el 5.

Problema de Puntos

Hoy en clase de problemas hemos hecho uno sobre puntos:

PUNTOS:

Necesitas papel punteado.

• El cuadrilátero de la figura tiene un área de 16,5 unidades cuadradas.
• El perímetro del cuadrilátero pasa por 9 puntos.
• El cuadrilátero contiene en su interior 13 puntos.

Dibuja tus propias formas e intenta hallar una relación entre el área, el número de puntos en el perímetro y el número de puntos dentro de cada figura.

Tras hacer varios dibujos y ordenar los datos que obtenía en una tabla... no llegue a ninguna conclusión.

Intenta hallar un resultado similar para una trama triangular. (Por supuesto, tendrás que redefinir tu unidad de área.)

Como para la trama de cuadrados no encontré ninguna relación, no lo intente con la triangular.

Y esto es todo. Saludos!

Funciones Polinómicas

Lo que hemos hecho hoy en clase ha sido corregir algunos ejercicios y después dimos algo de teoría:

Corrección de los ejercicios 43 y 44 de la página 174:

43) Representa la función.

Representación:

44) Representa esta función.

Representación:

Corrección de los ejercicios 5 y 6 de la página 179:

5) Representa, en unos mismos ejes, estas funciones y explica sus diferencias.

a) Y=2X b) Y=2X-3 c) Y=2X+1

Las diferencia es que aunque la pendiente en todos los casos es la misma (2X), el término independiente que acompaña a la función va variando.

6) Asocia cada recta con su expresión algebraica.

a) Y=2X+2 c) Y=-1/2

b) Y=-X-3 d) Y=-X

Solución:

A-4 B-2 C-no coincide con ninguna D-3

Y esta es la teoría que hemos dado sobre las funciones polinomicas:

FUNCIONES POLINÓMICAS DE 1er GRADO: Y= f (X)= mX+n

• m= pendiente de la función, es decir, la inclinación.

Si m=0 : f (X)= n es una función constante.

• n= punto de corte con el eje Y.

Si n=0 : f (x)=mX es una función lineal, es decir cuando la recta pasa por el origen.

• Si m y n son distitos de 0, f (X) es una funcion afín.

FUNCIONES POLINOMICAS DE 2º GRADO: Y= f (X)= aX²+bX+c

Su función es una parábola con dos ramas, una creciente y otra decreciente.

-ELEMENTOS:

• Vértice: punto donde la función pasa de ser creciente a decreciente o al revés.
• Eje de simetría: es una recta que pasa por el vértice y es paralela o coincidente al eje Y.

Ejemplo:

Y eso es todo. Bego no ha mandado tarea :D

ESTUPIDEZ

Hace falta ser estúpido por no decir cosas peores para hacer algo como esto grabarlo y encima subirlo a youtube . Ah y se ve que ese esta muy afligido por la muerte del conejo.... En fin...

EL CUBO PINTADO

Jueves = problemas, hoy nos ha tocado este:

-imagina que las seis superficies exteriores de un gran cubo se pintan de color negro.Este gran cubo, se corta despues en 4913 cubos (4913=17x17x17)

-Cuantos de estos 4913 cubos tienen:

.O caras negras?

.1 cara negra?

.2 caras negras?

.3 caras negras?

.4 caras negras?

.5 caras negras?

.6 caras negras?

Para mi lo mas facil fue abrir el cubo:

El cubo tiene 12 aristas

su volumen es de 4913 metros cubicos

tiene 6 caras y 8 esquinas

Lo primero que he hecho ha sido calcular el numero de cubitos en la superficie del cubo:

Sabemos en cada arista hay 17 cubitos,cuando vayamos a calcular la cantidad de cubitos de cada lado exterior tendremos que restarle 1 o 2 cubitos dependiendo del lado que sea, por lo tanto:

El cuadrado 1 tiene 17x16=272 cubitos ya que se le quitan 1 cubito de un lado para no contarlo 2 veces.

El cuadrado 2 tiene 17x17=289 cubitos.

El cuadrado 3 tiene 16x15=240

El cuadrado 4 tiene 15x15=255

El cuadrado 5 tiene 16x16=256

El cuadrado 6 tiene 16x16=256

Al sumarlo todo tendremos la cantidad de cubitos en toda la superficie exterior: Suma total=1568cubitos.

Ahora si restamos el numero total de cubitos en todo el cubo - el numero de cubitos de las 6 superficies exteriores obtendremos el nuemro de cubitos con 0 caras pintadas; 4913-1547=3366

Esta claro que los unicos cibitos con 2 caras pintadas pueden ser los que estan en la arista, descontando los 2 cubitos de los bordes por lo tanto 15x12=180 cubitos con 2 caras pintadas

Para los de 1 cara pintada....

180+8=188 4913-3366=1547 1547-188=1359 con 1 cara pintada

Y los de 3, como solo pueden serlos de las esquinas pues 8x1=8

Los de 4,5,6 son imposibles:)

RESULTADO:

con 0 caras negras: 3366

con 1 cara negras :1359

con 2 caras eagras :180

con 3 caras pintadas :8

El siguiente apartado no supe hacerlo...

No se si esta bien, igual me he confundido en algun calculo...

Esto es todo y mańana....... VIERNEEEEEEEES!!

Adios

PD: no debia de verse todo tan junto:(

Tema 10Funciones Polinomicas y racionales

Esta es parte de la tarea que corregimos hoy en clase.

Vuelta de vacaciones. Estudio de gráficas

Como veis, después de unas vacaciones, que se nos han hecho muy cortas, volvemos a la normalidad, y vuelta al blog! jajaja

Y hoy en clase lo que hemos hecho es empezar a corregir la tarea.

Era estudiar varias gráficas, y aquí voy a dejar las que hemos visto.

1º

1: Dom f = (- ∞ , 0] U [2, 5] U [6 , ∞)

Im f = [-1 , ∞)

2: Es discontinua. Continuidad = (- ∞ , 0] U [2, 5] U [6 , ∞)

Ptos discontinuidad = x=0 ; x=2 ; x=5 ; x=6

3: Cortes con los ejes -- eje x = (0,0) , (6,0)

eje y = (0,0)

4: Signo = (- ∞ ,0) : +

(2,5) : -

(6, ∞ ) : +

5: No es simétrica ni periódica

6: Creciente = (6,0) Máx = NO

Decreciente = (-∞,0) Min = (0,0) , (6,0)

Constante = (2,5)

7: Concavidad ( U) = (-∞, -3'5) U (-2'5,-1'5) U (6,6'5) U (7'5,8'3)

Convexidad = ( 3'5,-2'5) U (-1'5,0) U (6'5,7'5) U (8'3, ∞)

Ptos de inflexión = (-3'5,-1'4) ; (-2'5,1) ; (-1'5, 0,7) ; (6'5,0'5) ; (7'5,1'2) ; (8'3,2'4)

8: Como tenemos la gráfica dada, no es necesario hacer una tabla, pero en ese caso sería dar valores a la "x" y, mirando la gráfica, poner su correspondiente "y".

2º

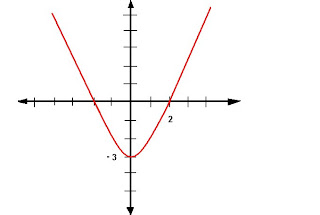
1: Dom f = R (todos los números reales)

Im f = [-3, ∞)

2: Es continua

3: Cortes con los ejes -- eje x = (-2,0) , (2,0)

eje y = (0, -3)

4: Signo = (-∞, -2) : +

(-2,2) : -

(2,∞) : +

5: Es simétrica respecto al eje "y".

No es periódica.

6: Creciente = (0, ∞)

Decreciente = (-∞, 0) Min = (0, -3)

7: Concavidad (U) = R (todos)

3º

1: Dom f = R

Im f = [-2,2]

2 : Es continua

3: Cortes con los ejes -- eje x = (-5 ,0) , (-2'5,0) , (0,0), (2'5,0) , (5,0)

eje y = (0,0)

4: Signo = + , - , +, - ...... cada 2'5

5: Es simétrica respecto al origen.

Es periódica de periodo 5, es decir, cada 5 puntos se repite todo el rato.

Bueeeeno, pues aquí nos hemos quedado en la clase de hoy.

Asi que mañana seguiremos corrigiendo chic@s!

Por lo tanto, hoy sin tarea :D