Vectores fijos y libres en el plano

Hola a todos.
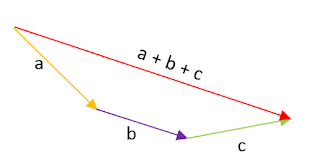
Os voy a explicar lo que dimos en clase.Empezamos:

• Un vector fijo , es un segmento orientado con origen en el punto A y el extremo del punto B.

Los elementos de un vector son:

• Módulo de un vector es la distancia que separa a su origen de su extremo.
• Dirección de un vector es la dirección de ka recta que pasa por su origen y por su extremo y la de todas sus paralelas.
• Sentido de un vector es el que queda determinado al ir desde el origen al extremo.

Las coordenadas del vector de origen el punto A( a1, a2) y del extremo el punto B (b1, b2) son las del extremo menos las del origen.


El módulo de un vector AB  dados 2 puntos.
 



Vector de posición:
Es cualquier vector fijo que tenga como origen el origen de coordenadas. Las coordenadas de un vector de posición coinciden con las coordenadas del extremo.

Vectores equipolentes:
Cuando tienen el mismo módulo, la misma dirección y sentido.



Vectores libres en el plano:
El conjunto formado por todos los vectores equipolentes a un vector fijo se denomina vector libre.

OPERACIONES CON VECTORES. COMBINACIÓN LINEAL

Buenas tardes! Hoy en clase de mates hemos explicado las páginas 138- 139 (excepto punto medio de un segmento) del libro.

En primer lugar, tenemos que recordar qué es un vector libre. ¿Os acordáis que lo dimos hace poco? Era una especie de representante de un conjunto de vectores equipolentes. Vamos a usar los vectores:

 u ⃗   = (u₁, u₂)

v ⃗=( v₁, v₂)

  #Suma de vectores libres

Algebraicamente:

u ⃗ +v ⃗  =(u₁+v₁,  u₂+v₂)

 Geométricamente: 

Aclaración: las coordenadas de un punto nos indican cuánto se mueven hacia la izquierda/derecha y arriba/abajo no el punto de comienzo ni de final.

#Producto de un número por un vector

Nº: K€R

 K u ⃗  = K (u₁, u₂)= (Ku₁, Ku₂)

 Al hacer esta multiplicación, el módulo va a cambiar ( si multiplicamos por 1 no). Además, si lo multiplicamos por un número negativo, cambiará el módulo pero también el sentido.

#Combinación lineal de vectores

Dos vectores,u ⃗   y  v ⃗, son linealmente dependientes (l.d) si tienen la misma dirección y sus coordenadas son proporcionales. 

- Ejemplo 1 :

u ⃗ = (2,4)  

    v ⃗ = (1,2)    Por lo tanto...  u ⃗= 2  v ⃗  sí son l.d

- Ejemplo 2:

u ⃗ = (2,4)  

    v ⃗ = (-1, -2)          Por lo tanto...  u ⃗= -2  v ⃗   sí son l.d

- Ejemplo 3:

u ⃗ = (2,4)  

    v ⃗ = (-1,2)    Por lo tanto...  NO son linealmente dependientes  

Combinación lineal (c.l): El vector w ⃗  es combinación lineal de los vectores u ⃗   y  v ⃗ si se pueden encontrar números reales tales que: w ⃗= au ⃗   + b v ⃗ 

Ejemplo:

¿w ⃗(3,4) es l.d  de u ⃗ (1,0) y  v ⃗ (0,1)?

w ⃗= 3(1,0) + 4( 0,1) = (3,0) + (0,4)= (3,4) 

TAREA: Pg 139 ejs 8, 9, 11. 

Además, recuerdo que el examen global de la 2ª evaluación es el miércoles 28 de marzo (dentro de una semana). Hay que estudiar desde los sistemas de ecuaciones hasta el tema anterior a los vectores ( los vectores no entran en esta evaluación?

¡Hasta mañana!

  

  

  

  

ECUACIONES TRIGONOMÉTRICAS

Hola chicos,

Os dejo este vídeo de Unicoos que explica, desde mi punto de vista, muy bien las ecuaciones trigonométricas que empecé yo a explicar el lunes en clase. Podéis pedir al profesor/a de guardia que lo pare e ir copiando en el cuaderno o podéis volver a verlo si es necesario. Las ecuaciones que tenéis que hacer están relacionadas con las ecuaciones del vídeo, son del mismo tipo. Es el ejercicio 90 de la página 114.

Ecuaciones Trigonométricas

Ecuaciones Trigonométricas

Una ecuación trigonométrica es aquella en la que la incógnita forma parte de una razón trigonométrica. 

Para resolver la ecuación trigonométrica la incógnita va a ser en este caso el ángulo.

Si conocemos la razón trigonométrica de un ángulo, para hallar el ángulo calculamos sus inversas:

                        Inversas

seno de alfa= x -------> arcseno de x= alfa

coseno de alfa= x ----> arccoseno de x= alfa

tangente de alfa= x---> arctangente de x= alfa

Ejemplo: 

3senx= 2

Antes de empezar el ejemplo recordamos... 

Vamos a tener que despejar la x (que es el ángulo). Pasamos el tres que multiplica a la x al otro lado dividiendo:

senx= 2/3 

Como es el seno el ángulo estará en el primer o segundo cuadrante ya que es positivo

x= arcseno 2/3

La x tiene dos posibles soluciones:

x= 42º + 360º K, (K perteneciente a la Z) 

x= 180- 42º + 360º K, (K perteneciente a la Z).

Deberes: Página 108 ejercicios 42 y 43.